Process calculus

In computer science, the process calculi (or process algebras) are a diverse family of related approaches for formally modelling concurrent systems. Process calculi provide a tool for the high-level description of interactions, communications, and synchronizations between a collection of independent agents or processes. They also provide algebraic laws that allow process descriptions to be manipulated and analyzed, and permit formal reasoning about equivalences between processes (e.g., using bisimulation). Leading examples of process calculi include CSP, CCS, ACP, and LOTOS.^[1] More recent additions to the family include the $\pi$ -calculus, the ambient calculus, PEPA and the fusion calculus.

1 Essential features
2 Mathematics of processes
3 Discrete and continuous process algebra
4 History
5 Current research
6 Software implementations
7 Relationship to other models of concurrency
8 References
9 Further reading

Essential features

While the variety of existing process calculi is very large (including variants that incorporate stochastic behaviour, timing information, and specializations for studying molecular interactions), there are several features that all process calculi have in common:^[2]

Representing interactions between independent processes as communication (message-passing), rather than as the modification of shared variables

Describing processes and systems using a small collection of primitives, and operators for combining those primitives

Defining algebraic laws for the process operators, which allow process expressions to be manipulated using equational reasoning

Mathematics of processes

To define a process calculus, one starts with a set of names (or channels) whose purpose is to provide means of communication. In many implementations, channels have rich internal structure to improve efficiency, but this is abstracted away in most theoretic models. In addition to names, one needs a means to form new processes from old. The basic operators, always present in some form or other, allow:^[3]

parallel composition of processes
specification of which channels to use for sending and receiving data
sequentialization of interactions
hiding of interaction points
recursion or process replication

Parallel composition

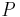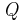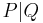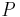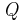Parallel composition of two processes $\mathit{P}$ and $\mathit{Q}$ , usually written $P \vert Q$ , is the key primitive distinguishing the process calculi from sequential models of computation. Parallel composition allows computation in $\mathit{P}$ and $\mathit{Q}$ to proceed simultaneously and independently. 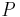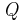But it also allows interaction, that is synchronisation and flow of information from $\mathit{P}$ to $\mathit{Q}$ (or vice versa) on a channel shared by both. Crucially, an agent or process can be connected to more than one channel at a time.

Channels may be synchronous or asynchronous. In the case of a synchronous channel, the agent sending a message waits until another agent has received the message. Asynchronous channels do not require any such synchronization. In some process calculi (notably the $\pi$ -calculus) channels themselves can be sent in messages through (other) channels, allowing the topology of process interconnections to change. Some process calculi also allow channels to be created during the execution of a computation.

Communication

Interaction can be (but isn't always) a directed flow of information. That is, input and output can be distinguished as dual interaction primitives. Process calculi that make such distinctions typically define an input operator (e.g. 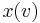$x(v)$ ) and an output operator (e.g. 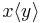$x\langle y\rangle$ ), both of which name an interaction point (here 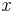$\mathit{x}$ ) that is used to synchronise with a dual interaction primitive.

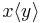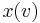Should information be exchanged, it will flow from the outputting to the inputting process. The output primitive will specify the data to be sent. In $x\langle y\rangle$ , this data is $y$ . Similarly, if an input expects to receive data, one or more bound variables will act as place-holders to be substituted by data, when it arrives. In $x(v)$ , $v$ plays that role. The choice of the kind of data that can be exchanged in an interaction is one of the key features that distinguishes different process calculi.

Sequential composition

Sometimes interactions must be temporally ordered. For example, it might be desirable to specify algorithms such as: first receive some data on 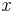$\mathit{x}$ and then send that data on 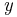$\mathit{y}$ . Sequential composition can be used for such purposes. It is well known from other models of computation. In process calculi, the sequentialisation operator is usually integrated with input or output, or both. For example, the process 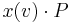$x(v)\cdot P$ will wait for an input on 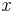$\mathit{x}$ . 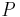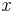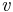Only when this input has occurred will the process $\mathit{P}$ be activated, with the received data through $\mathit{x}$ substituted for identifier $\mathit{v}$ .

Reduction semantics

The key operational reduction rule, containing the computational essence of process calculi, can be given solely in terms of parallel composition, sequentialization, input, and output. The details of this reduction vary among the calculi, but the essence remains roughly the same. The reduction rule is:

$x\langle y\rangle \cdot P \; \vert \; x(v)\cdot Q \longrightarrow P \; \vert \; Q[^y\!/\!_v]$

The interpretation of this reduction rule is:

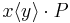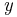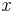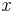The process $x\langle y\rangle \cdot P$ sends a message, here $\mathit{y}$ , along the channel $\mathit{x}$ . Dually, the process $x(v)\cdot Q$ receives that message on channel $\mathit{x}$ .
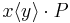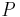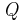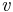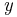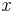Once the message has been sent, $x\langle y\rangle \cdot P$ becomes the process $\mathit{P}$ , while $x(v)\cdot Q$ becomes the process $Q[^y\!/\!_v]$ , which is $\mathit{Q}$ with the place-holder $\mathit{v}$ substituted by $\mathit{y}$ , the data received on $\mathit{x}$ .

The class of processes that 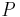$\mathit{P}$ is allowed to range over as the continuation of the output operation substantially influences the properties of the calculus.

Hiding

Processes do not limit the number of connections that can be made at a given interaction point. But interaction points allow interference (i.e. interaction). For the synthesis of compact, minimal and compositional systems, the ability to restrict interference is crucial. Hiding operations allow control of the connections made between interaction points when composing agents in parallel. Hiding can be denoted in a variety of ways. 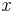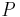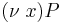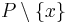For example, in the $\pi$ -calculus the hiding of a name $\mathit{x}$ in $\mathit{P}$ can be expressed as $(\nu\; x)P$ , while in CSP it might be written as $P \setminus \{x\}$ .

Recursion and replication

The operations presented so far describe only finite interaction and are consequently insufficient for full computability, which includes non-terminating behaviour. Recursion and replication are operations that allow finite descriptions of infinite behaviour. Recursion is well known from the sequential world. 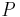Replication $!P$ can be understood as abbreviating the parallel composition of a countably infinite number of $\mathit{P}$ processes:

$!P = P \vert�!P$

Null process

Process calculi generally also include a null process (variously denoted as 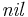$\mathit{nil}$ , $0$ , $\mathit{STOP}$ , $\delta$ , or some other appropriate symbol) which has no interaction points. It is utterly inactive and its sole purpose is to act as the inductive anchor on top of which more interesting processes can be generated.

Discrete and continuous process algebra

Process algebra has been studied for discrete time and continuous time (real time or dense time)^[4]

History

In the first half of the 20th century, various formalisms were proposed to capture the informal concept of a computable function, with μ-recursive functions, Turing Machines and the lambda calculus possibly being the best-known examples today. The surprising fact that they are essentially equivalent, in the sense that they are all encodable into each other, supports the Church-Turing thesis. Another shared feature is more rarely commented on: they all are most readily understood as models of sequential computation. The subsequent consolidation of computer science required a more subtle formulation of the notion of computation, in particular explicit representations of concurrency and communication. Models of concurrency such as the process calculi, Petri-Nets in 1962, and the Actor model in 1973 emerged from this line of enquiry.

Research on process calculi began in earnest with Robin Milner's seminal work on the Calculus of Communicating Systems (CCS) during the period from 1973 to 1980. C.A.R. Hoare's Communicating Sequential Processes (CSP) first appeared in 1978, and was subsequently developed into a fully-fledged process calculus during the early 1980s. There was much cross-fertilization of ideas between CCS and CSP as they developed. In 1982 Jan Bergstra and Jan Willem Klop began work on what came to be known as the Algebra of Communicating Processes (ACP), and introduced the term process algebra to describe their work.^[1] CCS, CSP, and ACP constitute the three major branches of the process calculi family: the majority of the other process calculi can trace their roots to one of these three calculi.

Current research

Various process calculi have been studied and not all of them fit the paradigm sketched here. The most prominent example may be the ambient calculus. This is to be expected as process calculi are an active field of study. Currently research on process calculi focuses on the following problems.

Developing new process calculi for better modeling of computational phenomena.

Finding well-behaved subcalculi of a given process calculus. This is valuable because (1) most calculi are fairly wild in the sense that they are rather general and not much can be said about arbitrary processes; and (2) computational applications rarely exhaust the whole of a calculus. Rather they use only processes that are very constrained in form. Constraining the shape of processes is mostly studied by way of type systems.

Logics for processes that allow one to reason about (essentially) arbitrary properties of processes, following the ideas of Hoare logic.

Behavioural theory: what does it mean for two processes to be the same? How can we decide whether two processes are different or not? Can we find representatives for equivalence classes of processes? Generally, processes are considered to be the same if no context, that is other processes running in parallel, can detect a difference. Unfortunately, making this intuition precise is subtle and mostly yields unwieldy characterisations of equality (which in most cases must also be undecidable, as a consequence of the halting problem). Bisimulations are a technical tool that aids reasoning about process equivalences.

Expressivity of calculi. Programming experience shows that certain problems are easier to solve in some languages than in others. This phenomenon calls for a more precise characterisation of the expressivity of calculi modeling computation than that afforded by the Church-Turing thesis. One way of doing this is to consider encodings between two formalisms and see what properties encodings can potentially preserve. The more properties can be preserved, the more expressive the target of the encoding is said to be. For process calculi, the celebrated results are that the synchronous $\pi$ -calculus is more expressive than its asynchronous variant, has the same expressive power as the higher-order $\pi$ -calculus, but is less than the ambient calculus.

Using process calculus to model biological systems (stochastic $\pi$ -calculus, BioAmbients, Beta Binders, BioPEPA, Brane calculus). It is thought by some that the compositionality offered by process-theoretic tools can help biologists to organise their knowledge more formally.

Software implementations

The ideas behind process algebra have given rise to several tools including:

Relationship to other models of concurrency

The history monoid is the free object that is generically able to represent the histories of individual communicating processes. A process calculus is then a formal language imposed on a history monoid in a consistent fashion.^[5] That is, a history monoid can only record a sequence of events, with synchronization, but does not specify the allowed state transitions. Thus, a process calculus is to a history monoid what a formal language is to a free monoid (a formal language is a subset of the set of all possible finite-length strings of an alphabet generated by the Kleene star).

The use of channels for communication is one of the features distinguishing the process calculi from other models of concurrency, such as Petri nets and the Actor model (see Actor model and process calculi). One of the fundamental motivations for including channels in the process calculi was to enable certain algebraic techniques, thereby making it easier to reason about processes algebraically.

References

^ ^a ^b J.C.M. Baeten: A brief history of process algebra, Rapport CSR 04-02, Vakgroep Informatica, Technische Universiteit Eindhoven, 2004
^ Benjamin Pierce: “Foundational Calculi for Programming Languages”, The Computer Science and Engineering Handbook, pp. 2190-2207, CRC Press, ISBN 0-8493-2909-4.
^ Baeten, J.C.M.; M. Bravetti (August 2005). "A Generic Process Algebra". Algebraic Process Calculi: The First Twenty Five Years and Beyond (BRICS Notes Series NS-05-3). Bertinoro, Forl`ı, Italy: BRICS, Department of Computer Science, University of Aarhus. http://www.brics.dk/NS/05/3/. Retrieved 2007-12-29.
^ Process algebra with timing: Real time and discrete time, JCM Baeten, CA Middelburg
^ Antoni Mazurkiewicz, "Introduction to Trace Theory", pp 3-41, in The Book of Traces, V. Diekert, G. Rozenberg, eds. (1995) World Scientific, Singapore ISBN 9810220588